background
It's often difficult for a (large) trader to execute efficiently on a CLOB (centralised limit order book).
If market participants detect a large block is being traded, prices will adjust in expectation (outside of the micro-scale, this is the market ecology theory for "trend following")
Always preferable to find a similarly large trader who is going the other way and meet them in the middle.
Trading has become increasingly fragmented, there are around 12 "national securities exchanges" for equities in the US, and dozens of ATSs.
market regulation: Reg NMS, MiFID
(all of the regulatory discussion below pertains to US "NMS stocks" and EU "liquid shares")
The spirit of both is to have a robust markets and a transparent price discovery process.
- Reg NMS (US securities):
- NBBO (national best bid and offer)
- OPR (order protection rule)
- largely, ATSs (alternative trading systems) can only piggy-back on the NBBO
- MiFID:
- strong demands for pre-trade transparency (doesn't stop quote fading 😢)
- dark pools (MTFs) operate under the "reference price waiver", but subject to 4,8% "double cap"
Post-trade transparency is a non-exemptionable requirement in both regimes
market regulation
Some of the regulation limits the activities of dark venues.
Some of the regulation makes them more necessary: smart order routing is very difficult to get right. In addition to the original "block trade" problem, it's also easy to get bitten by latency arb if I am forced to consume the NBBO first.
There are other clever (attempted) solutions, e.g. IEX's speed bumps and "crumbling order" signals. Auctions are similar to dark pools in that they can provide pre-trade privacy: see e.g. Budish's Frequent Batch Auctions
dark pools in the equities markets
- these days, 35-50% of US equities trading happens on dark venues (risen in last 15 years)
- only ~10% in EU (MiFID places caps on trading in non-lit venues), BUT:
- 15% in internalisers/broker crossing networks
- 25% in auctions (closing > periodic > opening)
There are (empirically justified) concerns that the opacity of dark pools also makes it hard to audit their fairness, and there have been numerous cases of dark pool operators misrepresenting their trading mechanisms.
- Barclays, Credit Suise fined $70mm, $85mm respectively in 2016
- around 6 SEC enforcement actions in 2017-8 (average penalty $17mm)
One could ask centralised operators to prove that they are conforming to some matching semantics, but it seems (?) impossible to prove that no information is being leaked, unless the information is never actually disclosed by the trader!
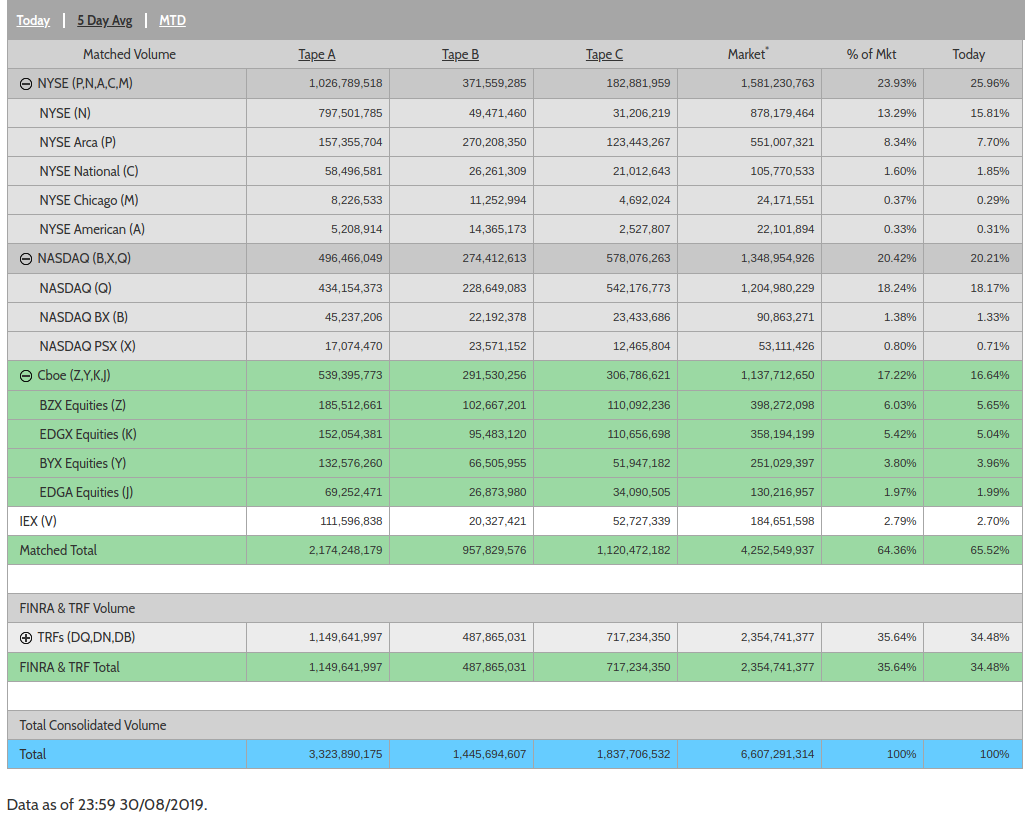
US market shares: source
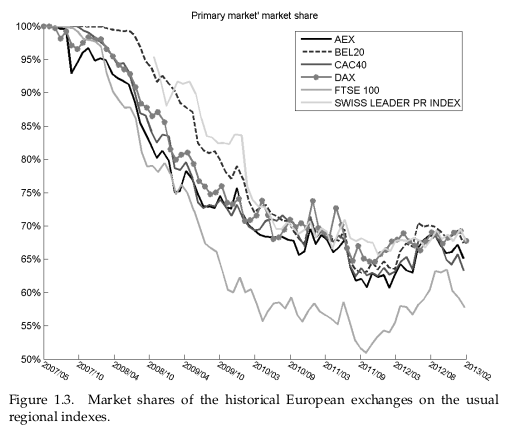
EU market shares: (Lehalle)
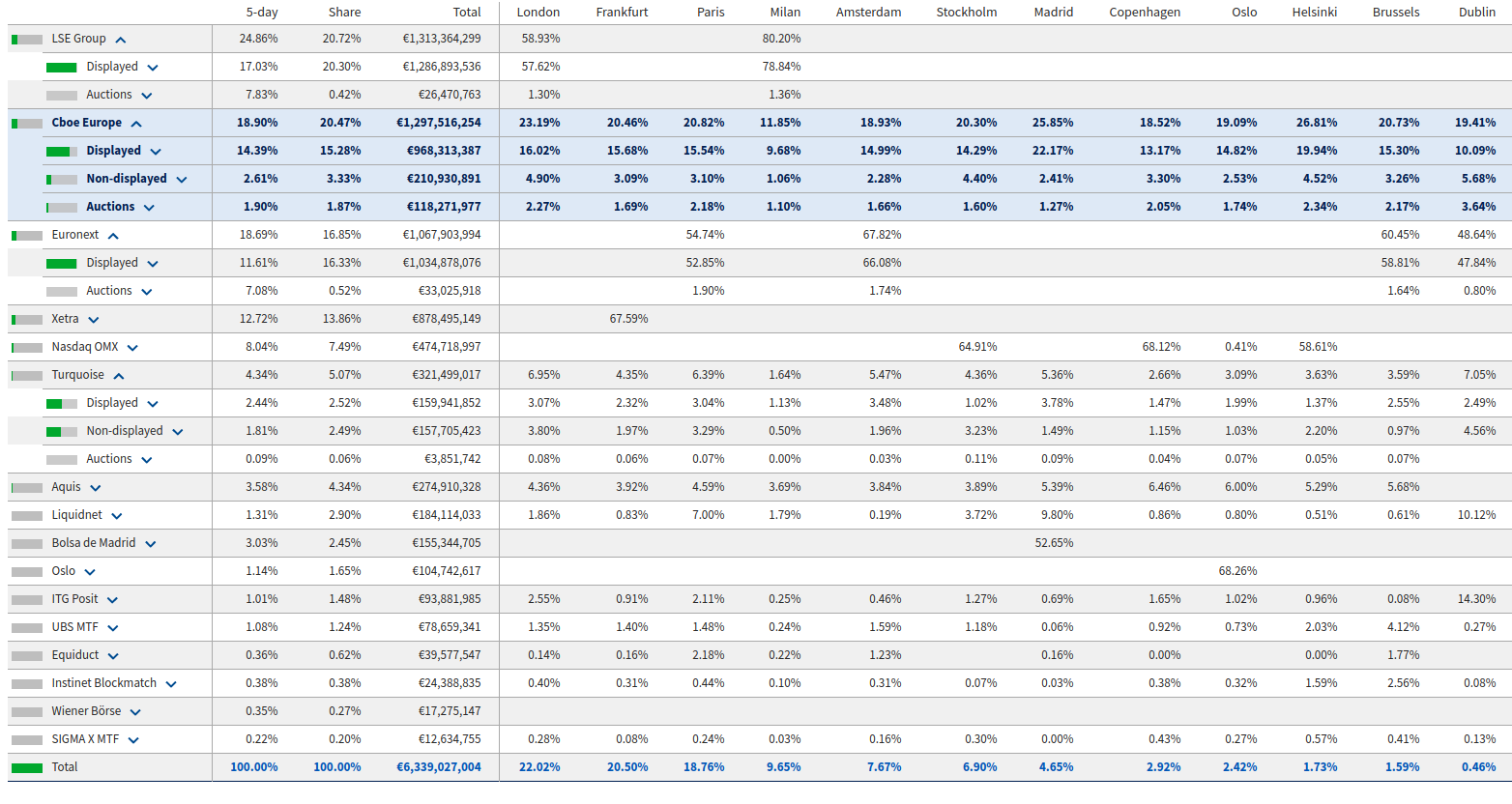
EU market shares: source
dark pool schemes
Wouldn't it be nice if we could have a dark pool without trusted parties, with clear semantics and no loopholes?
- I'll try to propose a bare-bones scheme, which (for simplicity) will have fixed order sizes and no price formation. This isn't as useless as it sounds:
- the former is OK because dark pools are mostly necessary for executing large trades (remainder can be executed lit)
- the latter is how existing dark pools already work (regulation)
- pre-trade privacy
- post-trade privacy (warning: illegal for listed securities! 👿)
- presented as a protocol extension to Zerocash
- ignores consensus layer and scalability issues
- no mention of cryptographic primatives or their feasibility
a dark pool scheme: setting
Suppose we have an existing set of coins \( \mathbb{C} \) and set of nullifiers \( \mathbb{S} \), from a scheme similar to Zerocoin or Zerocash.
A coin \( \mathbf{c} \in \mathbb{C} \) is a tuple \( \mathbf{c} = (r, v, \mathsf{sn}, \mathsf{cm}, \chi) \) where \( \mathsf{cm} := \mathsf{COMM}_r(\mathsf{sn} || v || \chi) \), where we have equipped coins with a value \( v \in \mathbb{N} \) and colour \( \chi \in \mathbb{N} \) (and corresponding proofs must attest that the values and colours on the input and output coins match, while the values and colours themselves can be kept private).
Remember: when the coin is minted only \( \mathsf{cm} \) is revealed, and when the coin is spent or poured, \( \mathsf{sn} \) is also revealed (and added to \( \mathbb{S} \)).
(throughout, I will quietly assume that this scheme is actually enriched with public-private key pairs, with poured coins getting encrypted to the recipient's key, and \( \mathsf{sn} \) is derived from a private key, commitment is nested, etc. etc.)
a dark pool scheme: exchange parameters
Our dark pool will have some fixed parameters:
- \( D \) : the maximum matching depth
- \( \left(\chi_i\right)^N_{i=1} \) : a set of \( N \) colours, the traded assets
- \( \chi_0 \) : the cash asset (e.g. DAI or another stablecoin)
- \( (p_i(t))^N_{i=1} \) : a price feed for every traded asset, in terms of \( \chi_0 \) (like in Reg NMS, MiFID: no price discovery here!)
- \( L \) : the lot size (all trades will be for this size) (intuition: quite big!)
- \( R \) : the order reserve ratio, which accounts for price drift between placing and settling an order (intuition: 105%)
- \( * \) : some realisation-specific parameters
a dark pool scheme: how to \( \tt MAKE \)
Let \( \chi_i \) be the asset I want to trade, and \( \delta \in \{ {\tt BUY}, {\tt SELL} \} \cong \{ 1, -1 \} \) be the order direction.
I generate an order secret \( s \) and an order salt \( u \), from which I derive an order nullifier \( \mathsf{on} := \mathsf{COMM}_s(u) \) and an order commitment \( \mathsf{oc} = \mathsf{COMM}(\mathsf{on} || \chi_i || \delta)\).
I also generate a public-private encryption key pair \( (k^{(i, \delta)}_{\mathsf{pk}}, k^{(i, \delta)}_{\mathsf{sk}}) \), using some encryption scheme where the public key is derived from the secret key, i.e. \( k^{(i, \delta)}_{\mathsf{pk}} = \mathsf{PKF}(k^{(i, \delta)}_{\mathsf{sk}}) \). Then, for every other possible asset-direction pair \( (j, \delta^\prime) \) I generate dummy public keys \( k^{(j, \delta^\prime)}_{\mathsf{pk}} = \mathsf{PRF}(s || \chi_j || \delta^\prime)\).
We call \( \mathsf{ks} = \left\{ k^{(j, \delta^\prime)}_{\mathsf{pk}} : j \in \{1, \ldots, N\}, \delta^\prime \in \{\tt BUY, SELL\} \right\} \) the key-set for the order.
n.b. \( \mathsf{PKF} \neq \mathsf{PRF} \) !!! Messages encrypted to a dummy key are noise. Key-privacy (in the sense of Bellare, Boldyreva, et al.) is also essential.
a dark pool scheme: how to \( \tt MAKE \) (cont'd)
Lastly, I need to produce a proof \( \pi^{\tt MAKE} \) that I know the \( r \) for some coin \( \mathbf{c} = (r, v, \mathsf{sn}, \mathsf{cm}, \chi^{\mathsf{offer}}) \), and moreover that:
- if \( \delta = \tt BUY \) then \( \chi^{\mathsf{offer}} = \chi_0 \) and \( v \geq L \) (collateralised if buying)
- if \( \delta = \tt SELL \) then \( \chi^{\mathsf{offer}} = \chi_i \) and \( v \geq \frac{L R}{p_i(\mathsf{t})} \), where \(\mathsf{t}\) is the current time (collateralised if selling)
- \( \mathsf{sn} \) is not in \( \mathbb{S} \) (coin not spent)
- \( k^{(j, \delta^\prime)}_{\mathsf{pk}} = \mathsf{PRF}(s || \chi_j || \delta^\prime)\) for all \( (j, \delta^\prime) \neq (i, \delta) \) (all but one key are dummies)
So far we have: \( {\tt MAKE}(\mathsf{t}, r, s, u, \mathsf{sn}, \mathsf{on}, \chi_i, \delta) \rightarrow (\mathsf{t}, \pi^{\tt MAKE}, \mathsf{sn}, \mathsf{oc}, \mathsf{ks}) =: \mathbf{o} \). The order will need one more component, but first, we will look at the orderbook.
a dark pool scheme: the orderbook
We maintain a list \( \mathbb{O} \), of order commitments and extra messages, as follows:
| \( \mathbf{o}_1 \) | \( \mathbf{o}_2 \) | \( \mathbf{o}_3 \) | \( \mathbf{o}_4 \) | \( \ldots \ldots \) | \( \mathbf{o}_D \) | \( \mathbf{o}_{D+1} \) | \( \mathbf{o}_{D+2} \) | \( \ldots \) |
|---|---|---|---|---|---|---|---|---|
| \( \) | \( m^2_1 \) | \( m^3_2 \) | \( m^4_3 \) | \( \ldots \ldots\) | \( m^D_{D-1}\) | \( m^{D+1}_{D}\) | \( m^{D+2}_{D+1}\) | \( \ldots \) |
| \( \) | \( \) | \( m^3_1 \) | \( m^4_2 \) | \( \ldots \ldots\) | \( \vdots \) | \( \vdots \) | \( \vdots \) | \( \ldots \) |
| \( \) | \( \) | \( \) | \( m^4_1\) | \( \ldots \ldots\) | \( m^D_3\) | \( m^{D+1}_4\) | \( m^{D+2}_5\) | \( \ldots \) |
| \( \) | \( \) | \( \) | \( \) | \( \ddots \) | \( m^D_2\) | \( m^{D+1}_3\) | \( m^{D+2}_4\) | \( \ldots \) |
| \( \) | \( \) | \( \) | \( \) | \( \ddots \) | \( m^D_1\) | \( m^{D+1}_2\) | \( m^{D+2}_3\) | \( \ldots \) |
- where \( m^{\mathsf{t}}_{\mathsf{f}} := \mathsf{ENC}\left(k^{(i(\mathbf{o}_{\mathsf{f}}), -\delta)}_{\mathsf{pk}}(\mathbf{o}_{\mathsf{f}}), \mathsf{on}(\mathbf{o}_{\mathsf{t}})\right) \) is the order nullifier of \( \mathbf{o}_{\mathsf{f}} \) encrypted to the key of \( \mathbf{o}_{\mathsf{t}} \) which corresponds to the asset and the (opposite) direction of \( \mathbf{o}_{\mathsf{f}} \).
a dark pool scheme: how to \( \tt MAKE \) (cont'd) (cont'd)
Thus the order must also contain
\[ \mathsf{ms} := \left\{ m^{\mathsf{t}} : \mathsf{t} \in \{ 1, \ldots, D-1 \} \right\} \]
called the message set: a list of \( D-1 \) encryptions of my order secret to each of the \( D-1 \) most recent orders, in each case to the public key corresponding to the asset \( \chi_i \) and direction \( -\delta \).
\( \pi^{\tt MAKE} \) must also be extended to also prove that \( m^{\mathsf{t}} = \mathsf{ENC}\left(k^{(i, -\delta)}_{\mathsf{pk}}\left(\mathbf{o}^{\mathsf{t}}\right), \mathsf{on} \right) \) for \( \mathsf{t} = 1, \ldots, D-1 \).
Finally we have: \( {\tt MAKE}(\mathsf{t}, r, s, u, \mathsf{sn}, \mathsf{on}, \chi_i, \delta) \rightarrow (\mathsf{t}, \pi^{\tt MAKE}, \mathsf{sn}, \mathsf{oc}, \mathsf{ks}, \mathsf{ms}) =: \mathbf{o} \).
\( \mathsf{sn} \) is added to \( \mathbb{S} \) to prevent this coin from being spent, \( (\mathsf{oc}, \mathsf{t}) \) is added to the set of "open orders", and \( \mathsf{ms} \) is added to the table.
a dark pool scheme: the \( \tt MATCH \)
Suppose I have previously made an order, which is currently at position \( n \) in the list:
| \( \mathbf{o}_1 \) | \( \mathbf{o}_2 \) | \( \mathbf{o}_3 \) | \( \mathbf{o}_4 \) | \( \ldots \) | \( {\color{blue}\mathbf{o}_n} \) | \( \ldots \) | \( \mathbf{o}_D \) | \( \mathbf{o}_{D+1} \) | \( \mathbf{o}_{D+2} \) | \( \ldots \) |
|---|---|---|---|---|---|---|---|---|---|---|
| \( \) | \( m^2_1 \) | \( m^3_2 \) | \( m^4_3 \) | \( \ldots \) | \( {\color{blue} m^n_{n-1}}\) | \( \ldots \) | \( m^D_{D-1}\) | \( m^{D+1}_{D}\) | \( m^{D+2}_{D+1}\) | \( \ldots \) |
| \( \) | \( \) | \( m^3_1 \) | \( m^4_2 \) | \( \ldots \) | \( {\color{blue} \vdots} \) | \( \ldots \) | \( \vdots \) | \( \vdots \) | \( \vdots \) | \( \ldots \) |
| \( \) | \( \) | \( \) | \( m^4_1\) | \( \ddots \) | \( {\color{blue} m^n_2} \) | \( \ldots \) | \( m^D_4\) | \( m^{D+1}_5\) | \( m^{D+2}_6\) | \( \ldots \) |
| \( \) | \( \) | \( \) | \( \) | \( \) | \( {\color{blue} m^n_1} \) | \( \ldots \) | \( m^D_3\) | \( m^{D+1}_4\) | \( m^{D+2}_5\) | \( \ldots \) |
| \( \) | \( \) | \( \) | \( \) | \( \) | \( \ddots \) | \( m^D_2\) | \( m^{D+1}_3\) | \( m^{D+2}_4\) | \( \ldots \) | |
| \( \) | \( \) | \( \) | \( \) | \( \) | \( m^D_1\) | \( m^{D+1}_2\) | \( m^{D+2}_3\) | \( \ldots \) |
Suppose I am able to decrypt the message \( m^n_1 \), i.e. our orders match, and I know the nullifier \( \mathsf{on}^\prime := \mathsf{on}(\mathbf{o}_1) \).
a dark pool scheme: the \( \tt MATCH \)
\( {\tt MATCH}\left(s, u, \mathsf{on}, \mathsf{on}^\prime\right) \rightarrow \left( \pi^{\tt MATCH}, \mathsf{on}, \mathsf{on}^\prime \right) \) where \( \pi^{\tt MATCH} \) proves that:
- for some order commitment \( \mathsf{oc} \) in \( \mathbb{O} \):
- I know all of the inputs to this computation: \( \mathsf{oc} = \mathsf{COMM}(\mathsf{COMM}_s(u) || \chi_i || \delta)\).
- for some order commitment \( \mathsf{oc}^\prime \) in \( \mathbb{O} \):
- I know all of the inputs to this computation: \( \mathsf{oc}^\prime = \mathsf{COMM}(\mathsf{on}^\prime || \chi_i^\prime || \delta^\prime)\).
- \( \chi_i = \chi_i^\prime \) (assets match)
- \( \delta \cdot \delta^\prime = -1 \) (directions match)
At time \( \mathsf{t} \), \( (\mathsf{on}, \mathsf{t}) \) and \( (\mathsf{on}^\prime, \mathsf{t}) \) are added to \( \mathbb{T} \), the list of order nullifiers.
again: I am omitting some details that elevate this from a \( \tt SPEND \) to a \( \tt POUR \): two new coin commitments added to \( \mathbb{C} \) (n.b. this requires another proof of encryption to ensure counterparty got paid!)
a dark pool scheme: the \( \tt KILL \)
We also want to be able to cancel orders, but I have to be able to prove that my order is not matchable.
\( {\tt KILL}\left( s, u, \mathsf{on} \right) \rightarrow \left(\pi^{\tt KILL}, \mathsf{on} \right) \), where \( \pi^{\tt KILL} \) proves that:
- for some order commitment \( \mathsf{oc} \) in \( \mathbb{O} \):
- I know all of the inputs to this computation: \( \mathsf{oc} = \mathsf{COMM}(\mathsf{COMM}_s(u) || \chi_i || \delta)\).
- \( \mathsf{COMM}_s(u) = \mathsf{on} \)
- for each \( m \) in the messages addressed to \( \mathsf{oc} \), either:
- \( \mathsf{DEC}\left(k^{(i, \delta)}_{\mathsf{sk}}\left(\mathbf{o}^{\mathsf{t}}\right), m \right) \) is garbage (order was not matchable); or
- \( \mathsf{DEC}\left(k^{(i, \delta)}_{\mathsf{sk}}\left(\mathbf{o}^{\mathsf{t}}\right), m \right) = \mathsf{on}^\prime \) and \( \mathsf{on}^\prime \in \mathbb{T} \) (order was cancelled or matched by someone else)
n.b. to penalise slow matchers (and spies 😲), we could strenghthen the second condition, adding a minimum match-response time and using timestamps.
(as in \( {\tt MATCH} \), we gloss over the settlement part: in this case, a new coin is minted to refund the owner of the cancelled order)
a dark pool scheme: notes
- n.b. \( \tt MATCH \) and kill are private not only w.r.t. order information, but also hide which order commitments they refer to
- this hinders metadata-based inference, esp. by other order makers
- n.b. as is, time-priority is not respected (matching is first-come first-served)
- could be repaired by adding a matching schedule, slowing down settlement a bit
- the matching depth limit \( D \) causes some "churn", limits the matchable counterparties for my order
- can create multiple order books with different parititions of assets and lot sizes (trades off anonymity set for scalability)
- required multiple ORd proofs of encryption/decryption 😬
- everything was assumed to be synchronous
next
- Cryptographers: are the zk-proofs feasible?
- \( N = 1\) and \( D = 5 \) would already be something
- what about \(N = 3\) and \( D = 12 \)?
- what type of zk-proof to use, what kind of encryption for efficient encryption proofs?
other work
- Parkes, Thorpe, Li (2015)
- focuses on Evaluator-Prover model (the operator can see all orders but must provide zero knowledge proofs of correct matching)
- also mentions Strong Secrecy, proposed approaches are:
- trusted computing
- having the operator be a (assumed non-colluding) consortium secure MPC
- also proposes batch auctions with time-lock puzzles
- RenVM RenEx
- sounds like the MPC approach (with its own consensus?)
- remarkably, can't find any literature on how it works, other than 2017 white paper
- Cyberian
- also MPC
- also no paper?
- seems less DEXy (trusted custodians for collateralisation and settlement)